Heli on teatavasti (või kuuldavasti) meid ümbritseva keskkonna (enamasti õhu) võnkumine. Mida intensiivsem võnkumine, seda valjumalt me tajume heli. Võnkumised ise on üldiselt ilusad ja ümmargused nagu allpool joonisel olev tavaline siinussignaal.
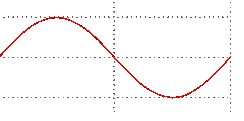
Arvuti ning ka kõik teised digitaalsed seadmed tegelevad hoopis numbrite, mitte võnkumistega, ning seetõttu tuleb arvutis töötlemiseks helisid kirjeldada numbrite abil. Selleks mõõdetakse sisendsignaali tugevust palju kordi sekundis ning salvestatakse saadud tulemus numbriliselt. Bittide arv määrab ära numbrite vahemiku, ehk kui palju erinevaid numbreid jääb vaikuse ning kõige tugevama signaali vahele.
Näiteks kõige lihtsam süsteem kasutaks ainult kahte numbrit -- 1 ja 0. Sellisel juhul oleks helisignaal kas sees või väljas. Sisse/välja lülitamise sagedus määrab helikõrguse. Üritades seda eelnevat siinussignaali sellisel moel sämpeldada, saame ühe korraliku nelinurksignaali:
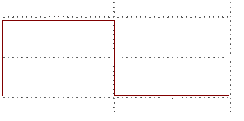
Esimesed moblad just nii tegidki ning kui see piiksumine mingi üldlevinud muusikapala meloodiat meenutas, olid kasutajad sillas. Nimetada võiks seda aga 1-bitiseks sämpliks.
Paraku puudub sellisel juhul igasugune dünaamika. Signaali ennast võib küll DA-muundur siluda ning uuesti ümmarguseks teha, aga heli tugevust muuta ei saa. Parema tulemuse saamiseks peame väärtuste vahemikku suurendama suurendades selleks bittide arvu. Arvuti nimelt salvestab kõik numbrid ühtede ning nullide jadana ning nende ühtede ning nullide (bittide) jada pikkus määrab kõige suurema arvu, mis sellisel moel on võimalik esitada. 0 on 0, 1 on 1, 10 on 2, 11 on 3, 100 on 4 jne. 16-bitise ühtede ning nullide jada puhul on maksimaalseks väärtuseks 65535. Kui negatiivsed arvud kah mängu tuua, siis 32767.
32 bitine
float on ujukomaarv, mis võimaldab veelgi suuremat numbrite vahemikku. Mida suurem on numbrite vahemik, seda täpsemalt on võimalik edastada helisignaalide erinevusi. Samas võtab helifail kõvakettal rohkem ruumi ning arvutamine nõuab arvutilt suuremat jõudlust ning ka mälu. Samuti ei pruugi sisendsignaal olla piisavalt kvaliteetne, et nii suurt bittide arvu õigustada kuna enamus lisatud bittidest kuluvad sisendsignaalis oleva müra registreerimiseks. CD-de puhul kasutatakse näiteks kõigest 16 bitti.
Pakuks välja, et juhul kui masin välja veab sobib töötlemiseks 32 bitine
float ning lõpptulemusele piisab 16-bitist. 32-bitine
float vähendab helisignaali töötlemisel muidu tekkivaid kadusid.
See siis minu poolne teoreetiline jutt. Eks praktikud oskavad öelda, mis nad tegelikult kasutavad


